LEON

《浙大 数据结构》树

2021.10.09

引子

查找Searching：根据某个给定的关键字K，从集合R中找出关键字与K相同的记录。

  • 静态查找：集合中的记录是固定的。没有插入和删除操作，只有查找。
  • 动态查找：集合中的记录是动态变化的，除查找还可能发生插入删除。

顺序查找

  • 创建
typedef struct Lnode *List;
struct Lnode{
    ElementType Element[MAXSIZE];
    int length;
}
  • 无哨兵
int SequentialSearch(List Tbl, ElementType K)
{
    int i;
    for(i = Tbl->Length; i>0 && Tbl->Element[i] != K; i--);
    return i;
}
  • 有哨兵
int SequentialSearch(List Tb1, ElementType K)
{
    int i;
    Tb1->Element[0] = K; // 建立哨兵
    for(i = Tb1->length; Tb1->Element[i] != K; i--);
    return i;
}

算法：

int BinarySearch(List Tbl, ElementType K) 
{
    int left, right, mid, NoFound=-1;
    left = 1;
    right = Tbl->Length; 
    while (left <= right) 
    {
        mid = (left+right)/2;
        if( K < Tbl->Element[mid])
            right = mid-1;
        else if( K > Tbl->Element[mid])
            left = mid+1;
        else
            return mid;  /*查找成功，返回数据元素的下标*/
    }
    return NotFound; /*发生边界错位，查找不成功，返回-1*/ 
}

11个元素的二分查找判定树：

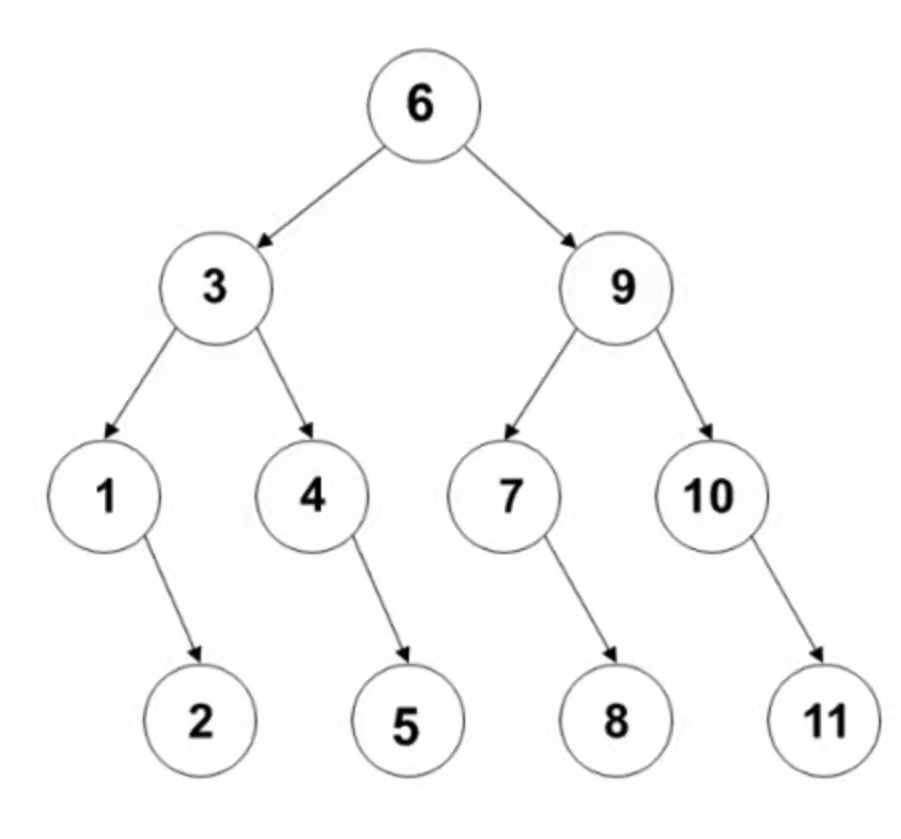
Untitled

  • 判定树上每个结点需要的查找次数刚好为该结点所在的层数
  • 查找成功时的查找次数不会超过判定树的深度
  • n个结点的判定树的深度为$log_2n+1$（取整）
  • 平均查找次数ASL = (44+43+2*2+1)/11

树 Tree

树的定义：

  • 树：n(n≥0)个结点构成的有限集合
  • 空树、非空树、根、子树
  • 子树是不相交的
  • 除根结点外，每个结点有且仅有一个父结点
  • 一颗N结点的树有N-1条边

树的基本术语：

  • 结点的度(Degree)：结点的子树个数
  • 树的度：树的所有结点中最大的度数
  • 结点的层次(Level)：规定根结点在1层， 其它任一结点的层数是其父结点的层数加1。
  • 树的深度(Depth)：树中所有结点中的最大层次是这棵树的深度。
CS